Hilbert's Curve

Pretty, isn’t it? But what is it?

Start with a U

then make four copies, glued in a U, shown in yellow and blue

and repeat

and repeat

and repeat

and repeat

and repeat and repeat til the curve fills the plane.

A bit hard to see. What if the curve wasn’t always black? What if it changed, from start to end?

Start small

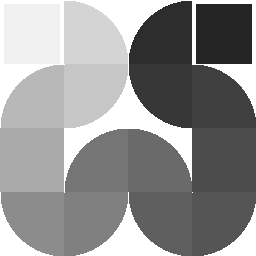
then repeat

and repeat

and repeat

and repeat

and repeat and repeat til the curve fills the plane.

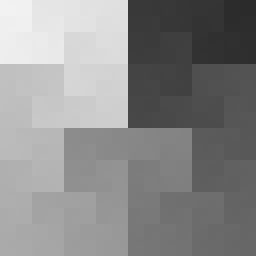
Now you see some of the majesty of Hilbert’s curve.

It is difficult, though, to see the subtle gradations of an infinite thing. This cannot be fixed; there is too much to see.

But we can try to see more.

Color it with every hue across the rainbow

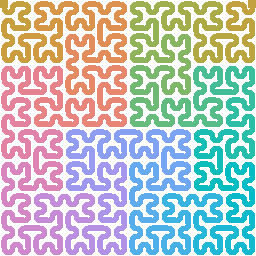
and repeat the curve

and repeat

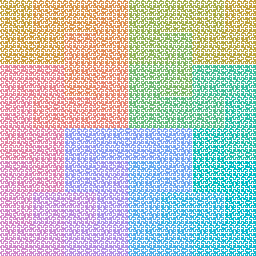
and repeat and repeat til the curve fills the plane.

Still so hard to see the details.

We’ve varied the lightness, and we’ve varied the hue, but neither revealed enough of the curve. So let’s vary them together, once around the hue and thrice around the lightness.

hue = 2πh
lightness = 3 |(h % 2/3) - 1|

It’s still hard to grasp that the curve’s detail is infinite, that what we see is only as much as one can see with so many pixels and so many colors. But the thing we can see, approximate though it may be, is beautiful.