Dominoe Computer

Suppose you have a whole bunch of dominoes that spring back up precisely three seconds after they’ve fallen down. Can you build a computer out of them?

---

It turns out that you can. But let’s start out by reasoning about the basics. To keep things simple, assume we have a big flat 2d floor on which to stand the dominoes. When playing with dominoes, the typical thing you do is put them in a line on the floor, and knock one over. Let’s call the line of dominoes a stream, and say that as they fall, a wave of falling dominoes travels down the stream. We’re supposed to be modeling a computer, so let’s say that a wave represents a 1 and the lack of a wave represents 0. Of course we can connect several streams together, so call a bunch of connected streams with some waves a circuit.

What sorts of circuits can we build? Let’s start simple. The most basic thing we can do with a stream is put a fork in it. Here’s a diagram:

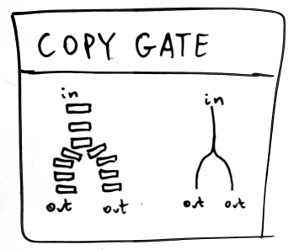
On the left is a picture of what the tops of the dominoes would look like, and on the right is a more abstract representation. I’m lazy about drawing, so we’ll use only abstract drawings from now on. I’ve labelled this circuit COPY GATE because if a wave comes down from ‘in’, it will be duplicated to each ‘out’. Hence we can take a bit sequence – that is, a sequence of waves and lack of waves – and duplicate it.

Ok, so that’s what a fork does. Well, at least that’s what it does if the wave is coming towards the fork. If we instead put that circuit upside down, we get an OR GATE instead:

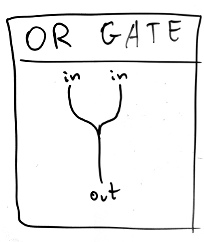
There’s a weakness to our circuits so far: they can duplicate 1s, but can’t produce any if there are none to start with. Fortunately we can produce an infinite sequence of 1s with a simple loop. Since the dominoes stand back up, a wave in a loop (of sufficient circumference) will circle it forever, and a COPY gate will emit a 1 each time it goes around. Adjusting the circumference of the loop controls the timing of the sequence.

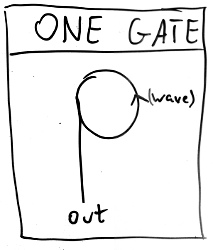
This can easily be extended to implement memory. In the circuit below, the left input is used to “set” the memory, after which the output is a sequence of 1s; and the right input is used to “unset” it, returning the output to 0.

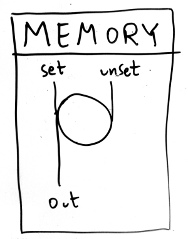
It’s also possible to build a diode; a circuit that allows “current” (i.e. waves) in one direction but not the other. Here a wave from the left will run into itself and “cancel out”, while an input from the top will continue on to the left unimpeded.

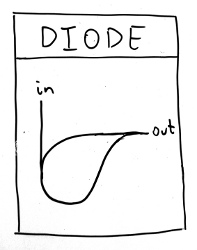
We can use a diode and a 1 input to construct a not gate. To do so, you have to be very careful about the delays that streams introduce, just like in a real computer. I’ve labelled parts of this circuit with numbers indicating how many seconds a wave should take to traverse them. There’s also two little boxes; these don’t correspond to anything physical, they just mark interesting locations where waves in opposite directions will cancel out.

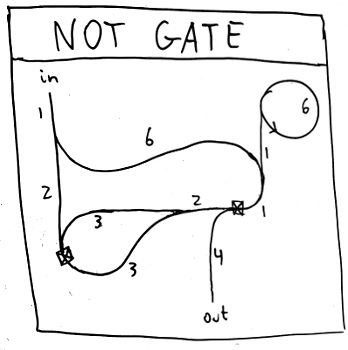
Now we have both OR and NOT gates. It’s well known that these gates together are universal, meaning that they can be combined to construct any logic gate. For instance, you can construct AND because x AND y is the same as NOT ((NOT x) OR (NOT y)). (It’s important that we have a ONE and COPY gate too, though those are usually taken for granted.) Thus we can build arbitrary logic gates.

Actually, I just lied. Do you see the hidden assumption?

Take a few minutes and think about it: why aren’t the gates I’ve described so far really universal?

---

When combining various circuits, it’s generally assumed that you can attach any circuit’s output to any other circuit’s input. But can we do that? The floor we’re placing dominoes on is 2-dimensional, and we can’t just have two streams cross because they’d crash into one another.

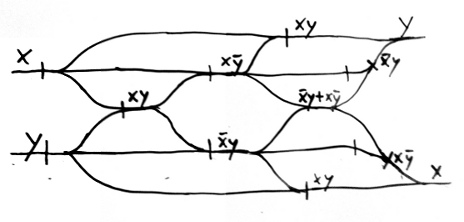
Fortunately there’s a workaround. There’s a circuit made up of OR and NOT gates whose outputs are its inputs, but swapped. Below is a picture. The inputs are labelled x and y, and intermediate values are labelled. Juxtaposition means AND, + means OR, and a bar on top of a letter means NOT. Streams splitting and joining together mean COPY and OR gates, as you would expect, and each veritcal bar is a NOT gate. By using this circuit we can swap streams, so with enough of them we can arrange streams however we need to, and so these circuits really are universal.

Therefore you can make memory and arbitrary logic gates out of stand-up-again dominoes, and, with enough patience, a general-purpose computer.