About Me
Archive
- Blackout
- Faster Than Light
- Hex Board
- Invariants
- Listening To OEIS
- Logic Gates
- Penrose Maze
- Syntactic Sugar
- Terminal Colors
Notes
Puzzles
Tree Editors
Programming
- Imagining a Language without Booleans
- Typst as a Language
- A Twist on Wadler's Printer
- Preventing Log4j with Capabilities
- Algebra and Data Types
- Pixel to Hex
- Linear vs Binary Search
Physics
Math
- Traffic Engineering with Portals, Part II
- Traffic Engineering with Portals
- Algebra and Data Types
- What's a Confidence Interval?
- Imagining a Language without Booleans
- JJ Cheat Sheet
- Typst as a Language
- A Twist on Wadler's Printer
- Space Logistics
- Hilbert's Curve
- Preventing Log4j with Capabilities
- Traffic Engineering with Portals, Part II
- Traffic Engineering with Portals
- Algebra and Data Types
- What's a Confidence Interval?
- Uncalibrated quantum experiments act clasically
- Pixel to Hex
- Linear vs Binary Search
- There and Back Again
- Tree Editor Survey
- Rust Quick Reference
- The Prisoners' Lightbulb
- Notes on Concurrency
- It's a blog now!
All Posts
Linear vs Binary Search
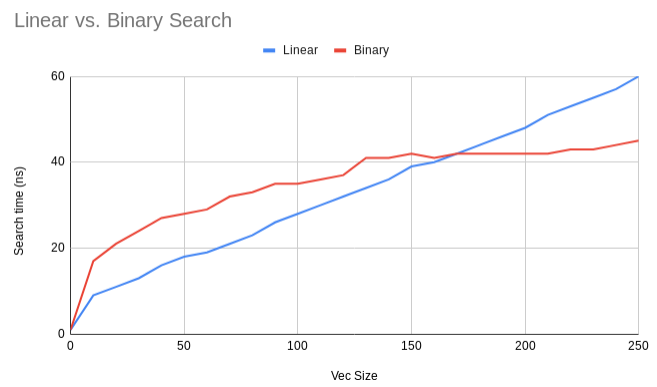
Linear search is faster than binary search for integer arrays with less than 150 elements.
In an algorithms class, you learn that merge sort has running time O(N*logN) while insertion sort has running time O(N²). This implies that in the limit, as the size of the list you’re sorting gets arbitrarily large, merge sort will be faster than insertion sort. (And furthermore, it will win out by an arbitrarily large amount if the list gets large enough.)
But it doesn’t say anything about which algorithm is faster for small lists. In fact, insertion sort is faster than merge sort for small lists in practice. As a result, serious sorting algorithms like Timsort use an asymptotically-fast sort like merge sort for large lists, but fall back to insertion sort for lists with fewer than 64 elements or so.
What about searching a sorted list? Binary search is O(logN) while linear search is O(N). But linear search is faster for smaller lists because it has less overhead and causes fewer branch mispredictions. So how large does your list have to be for linear search to be faster?
The last time I searched for this, I came up fairly empty handed, so I benchmarked it myself. But apparently I was bad at searching, so here is a blog post very similar to this one that comes to a similar conclusion. Alternatively, if you want to see a benchmark of very fast vectorized binary searching, look here.
To benchmark this, I wrote totally naive Rust code for linear search, and compared it to Rust’s builtin binary_search method. Source code is below.
I found linear search to outperform binary search on arrays of integers with fewer than about 150 elements. Here’s a graph. Runtime is measured as the average wall clock time in ns taken to search through an array of the given size. Each run is performed a thousand times over a million arrays and averaged to smooth out meaningless variation, though it’s still fairly bumpy.
You can see that the theory is born out quite well: linear search’s graph looks quite linear and binary search’s graph looks quite logarithmic.
//! Time linear vs. binary search.
//! Turning point: 150 elements.
use rand::random;
use std::cmp::Ordering;
use std::time::SystemTime;
fn random_vec(vec_len: usize) -> Vec<u8> {
let mut vec: Vec<u8> = (0..vec_len).map(|_| random()).collect();
vec.sort();
vec
}
/// Construct random vectors, each together with a random value to search for.
fn random_vecs(num_vecs: usize, vec_len: usize) -> Vec<(u8, Vec<u8>)> {
(0..num_vecs)
.map(|_| (random(), random_vec(vec_len)))
.collect()
}
fn linear_search(key: &u8, vec: &[u8]) -> Result<usize, usize> {
for (i, elem) in vec.iter().enumerate() {
match elem.cmp(&key) {
Ordering::Less => continue,
Ordering::Equal => return Ok(i),
Ordering::Greater => return Err(i),
}
}
Err(vec.len())
}
/// Time a function, returning both the result of calling the function and the
/// number of ms it took.
fn timed<T, F: FnOnce() -> T>(func: F) -> (T, u128) {
let start = SystemTime::now();
let answer = func();
let duration = start.elapsed().unwrap();
(answer, duration.as_millis())
}
fn run(num_vecs: usize, vec_len: usize, iterations: usize) -> usize {
let vecs = random_vecs(num_vecs, vec_len);
let (linear_total, linear_time) = timed(|| {
let mut total: usize = 0;
for _ in 0..iterations {
for (i, vec) in &vecs {
match linear_search(i, &vec) {
Ok(i) | Err(i) => total += i,
}
}
}
total
});
let (binary_total, binary_time) = timed(|| {
let mut total: usize = 0;
for _ in 0..iterations {
for (i, vec) in &vecs {
match vec.binary_search(i) {
Ok(i) | Err(i) => total += i,
}
}
}
total
});
let linear_time = linear_time * 1000000 / num_vecs as u128 / iterations as u128;
let binary_time = binary_time * 1000000 / num_vecs as u128 / iterations as u128;
let gibberish = linear_total + binary_total;
println!("{}\t{}\t{}", vec_len, linear_time, binary_time);
gibberish
}
fn main() {
println!("(Times are in ns.)");
println!("Len\tLinear\tBinary");
// `gibberish` computes... something... from the array,
// so that rustc doesn't optimize away the whole program.
let mut gibberish: usize = 0;
for len in (0..256).step_by(10) {
gibberish += run(1000000, len, 1000);
}
println!("Done ({})", gibberish);
}