About Me
Archive
- Blackout
- Faster Than Light
- Hex Board
- Invariants
- Listening To OEIS
- Logic Gates
- Penrose Maze
- Syntactic Sugar
- Terminal Colors
Notes
Puzzles
Tree Editors
Programming
- Typst as a Language
- A Twist on Wadler's Printer
- Preventing Log4j with Capabilities
- Algebra and Data Types
- Pixel to Hex
- Linear vs Binary Search
Physics
Math
- Lindenmayer Systems
- Traffic Engineering with Portals, Part II
- Traffic Engineering with Portals
- Algebra and Data Types
- What's a Confidence Interval?
PL Design
- Lindenmayer Systems
- Imagining a Language without Booleans
- JJ Cheat Sheet
- Typst as a Language
- A Twist on Wadler's Printer
- Space Logistics
- Hilbert's Curve
- Preventing Log4j with Capabilities
- Traffic Engineering with Portals, Part II
- Traffic Engineering with Portals
- Algebra and Data Types
- What's a Confidence Interval?
- Uncalibrated quantum experiments act clasically
- Pixel to Hex
- Linear vs Binary Search
- There and Back Again
- Tree Editor Survey
- Rust Quick Reference
- The Prisoners' Lightbulb
- Notes on Concurrency
- It's a blog now!
All Posts
Space Logistics
You know how you start a Factorio game with some friends, and play with the Space Exploration and Krastorio2 mods, and soon you’re 123 hours into the game and your factory spans several planetary bodies and you’re trying to figure out how to efficiently route arbitrary sets of resources between planets?
No? Maybe that’s just a me problem. But please, consider staying for the algorithms. By trying to do logistics in space we’ll end up with something like min-flow but on a tree.
The Problem
Here’s the problem statement:
You have a tree of locations. Each location has an integer associated with it; if it’s positive it’s called the location’s supply, and if negative it’s demand. If possible, find a non-negative flow for each edge such that all of the demands are satisfied after moving the supplies according to the flow. (The flow along an edge can be in either direction.) If no such flow exists, find one that satisfies as much as possible of the demands.
In reality, there’s more than one resource type, so one planet might have a supply of 5,000 iron but a demand for 3,000 copper. Fortunately, this can be viewed as two separate problems: finding the flow for iron and finding the flow for copper. So we only need to think about what to do for a single resource type.
What makes this problem manifest in Space Exploration Factorio? There are two key factors that cause it, and these factors might not show up until later in the game. The first is that there must be multiple sources (supplies) and sinks (demands) for the same resource; otherwise the problem is easy because there’s only one path for each resource. The second factor is that you are sending resources through intermediate locations, not directly from source to sink. (This comes about when you start using space elevators and spaceships instead of delivery cannons and/or rockets, for efficiency.)
Let’s walk through some potential solutions to this problem. The first couple won’t work, but that’s ok, we’ll learn something. I totally picked these bad solutions for exposition only; I certainly didn’t think they were great for a while before noticing the flaws. Nope, not me.
Solution: Temperature Gradients?
The rate of temperature flow from A to B is proportional to the difference in temperature between A and B.
For example, say you have a radiator that stays at exactly 100 degrees, and a perfectly insulated house that starts at 60 degrees, and it takes an hour for the house to heat up to 70 degrees. How much will the house heat up in the subsequent hour? Well, in the first hour the temperature difference was 100-60=40 degress, and in the next hour the temperature difference is 100-70=30 degrees. (This is an approximation. It wasn’t 60 degrees for the whole first hour, but neither of us wants to do calculus and this simplification doesn’t change the answer much.) Since the temperature difference went from 40 degrees to 30 degrees, the change in temperature will be 3/4 of what it was in the first hour, so it will rise by 3/4 * 10 = 7.5 degrees, ending at 77.5 degrees after the second hour.
Anyhow, let’s make iron flow the way that temperature does!
Here’s our tree of locations:
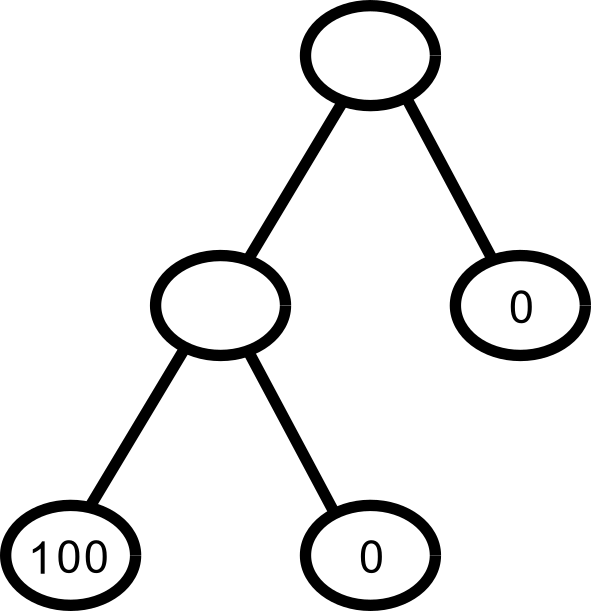
Say the bottom-left location is a planet with 100 iron available, and no matter how much you take from it it will immediately replenish itself to 100 iron. And the bottom-right and rightmost locations are planets with 0 iron, and if you give them any iron they will immediately eat it and turn it into cogs or something. And the other two locations are orbits we can route through.
(You may notice that this doesn’t match the problem statement above: the problem statement has demands be negative numbers, but here the demanding nodes are numbered 0. This is because the simplest way to do temperature gradient is to count the quantity of the resource, which is never negative. There’s a general lesson here: it’s sometimes best to slightly change the problem statement to match a potential solution, so long as it works for the real underlying problem you’re trying to solve.)
So we route the iron through these locations the way that heat flows: we compute the difference in how much iron each has, and make the flow proportional to that. If you do this, the system will reach a steady state that looks like this:

Notice that the flow on each edge is proportional to the difference between its locations, and that the in-flow of each location is perfectly balanced with its out-flow. This is how you can tell it’s a steady state. It’s like the steady state a drafty house will reach, with the draftier rooms being colder and the rooms with radiators being warmer.
While this is a very elegant solution, it’s not actually a great way to route Factorio resources. The situation above works pretty well, but let’s consider another one. It also looks like this to start:

But this time, say that the rightmost location isn’t actually an iron sink, it’s just a place that doesn’t have or care about iron. So you can give it iron, and then it will have iron but not do anything with it. Here’s what the steady state looks like in this case:

We filled the upper part of the tree with iron despite the fact that nothing up there wants it. If it were just iron this wouldn’t be so bad, but we’re going to be doing this for every resource type at once and don’t really want hundreds of kinds of resources piling up for no reason.
So let’s try something completely different.
Solution: Aggregate Supply&Demand?
“Look,” past me says, “it’s a tree. Trees are easy. A tree has a surplus if, when you add all of its supplies and subtract its demands, that total is positive. And it has a deficit if the total is negative. To calculate the flow along an edge, imagine cutting that edge. This splits the tree into two trees. If one of them has a deficit and the other has a surplus, there’s flow along the cut edge from the surplus to the deficit.”
“BAM. Solved,” he declares.
“A beautiful solution,” current me says, “let’s try it on a trivial example. Not to try to disprove it or anything, just to admire how wonderfully this elegant and obviously correct solution works. Here we go: a tree with two sources and one sink.”
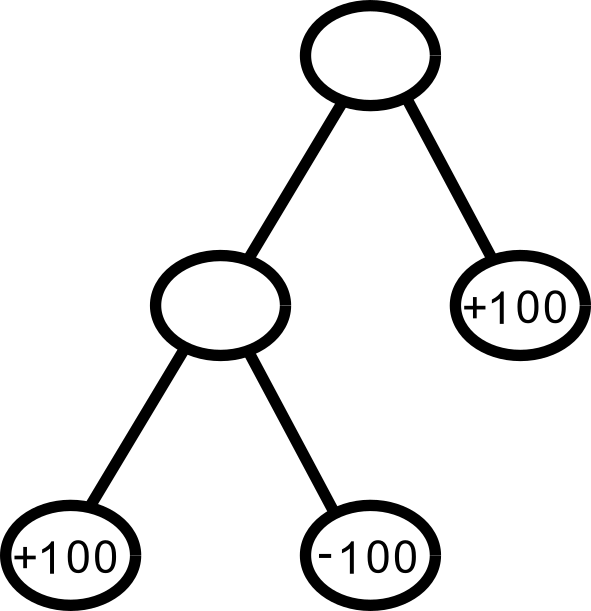
“And we consider an edge, and compute its flow. This edge separates a tree with a surplus of 100 from a tree with a suplus of zero:”

“So… no flow there. The 4-node tree already has enough supply to meet its own demand, so there’s no need to take from the single-node tree’s source to help it. Let’s now check that the demand is met by the other source, by considering this other edge:”

“Uh oh. This edge also separates a tree with a surplus of 100 from a tree with a surplus of zero, so it also has zero flow.”
“Each source sees that the other source could handle the demand, so it doesn’t bother to do anything itself. There’s some sort of life lesson in there. Anyway, this definitely isn’t a solution to routing,” I continue.
“Also, I appear to have gotten myself trapped inside quotes. Let’s see if a section header can break me out.”
An Actual Solution
I’ve escaped! Ok, back to the thing.
Here’s the actual solution I came up with:
- For each subtree, from the bottom up, add up all of the supplies and demands in that subtree. If the total is positive, it’s called a surplus and if it’s negative it’s called a deficit. For example, if a subtree has three locations, with supply 4, demand 10, and supply 1, then that subtree has a deficit of (positive) 5.
- For each non-leaf location, from the root down, compute its satisfaction or dissatisfaction. Start with the location’s own supply, or 0 if instead it has a demand. Then for each of its children that have a deficit, subtract that deficit. Finally, if its parent is dissatisfied, subtract that dissatisfaction. (Altogether: the location’s supply, minus its childrens’ deficits, minus it’s parent’s dissatisfaction.) If this total is positive, it’s called the location’s satisfaction, and if it’s negative it’s called a dissatisfaction. For example, say a location has a supply of 10, a child with surplus 333, a child with deficit 6, and a parent with a dissatisfaction of 5. Then that location’s total is 10 - 6 - 5 = -1, so it has a dissatisfaction of 1.
- Compute the flow as follows. Down flow is easy: if a location has a deficit of N, then there’s flow of N from its parent to it. (The definition of “deficit” implies the whole subtree needs outside help.) Up flow is trickier. There’s a flow from a child A to its parent B iff A has a surplus and B is dissatisfied. The magnitude of this flow is the dissatisfaction of B.
If it’s possible to satisfy the tree’s demands, this algorithm will do so precisely. If it’s not possible, it will suggest flows that aren’t possible to achieve, but attempting to do so will at least route all of the available supplies to demands. And it prefers to keep a subtree’s supplies within that subtree.
Let’s see it in action. Start with one source and two sinks:
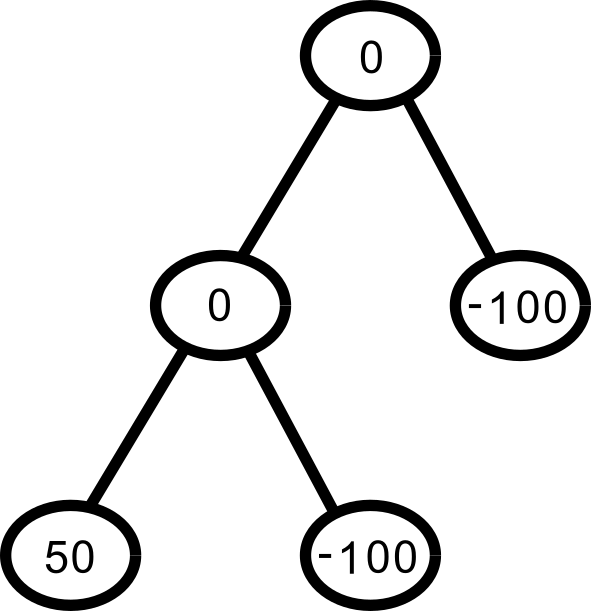
Add up all of the supplies and demands, to get a surplus/deficit for each location in blue:

Now compute the satisfaction for each location, in magenta:
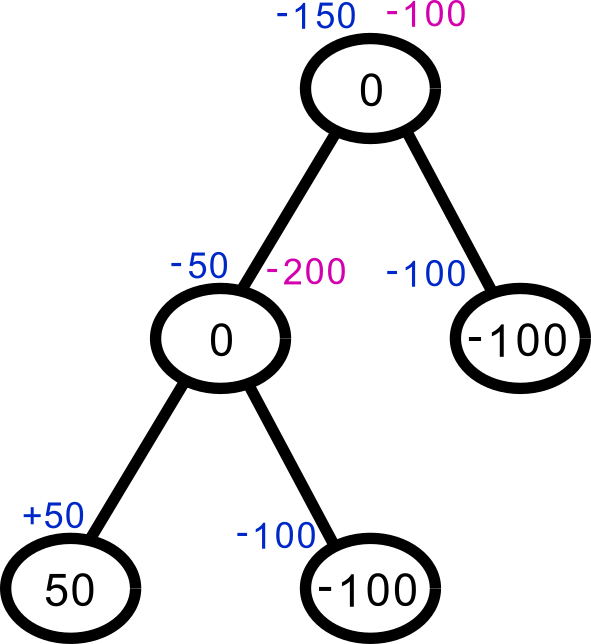
Finally, compute the flow along each edge, in green. There’s not nearly enough supply to meet the demand, so a lot of these flows are, uh, ambitious:
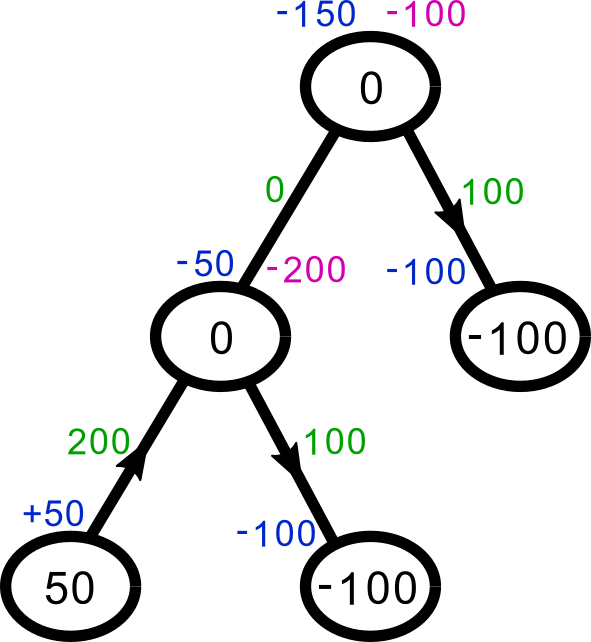
This example shows interesting behavior if the supply of the middle location increases. When it gets high enough that it has a surplus, it starts sending resources to the root:
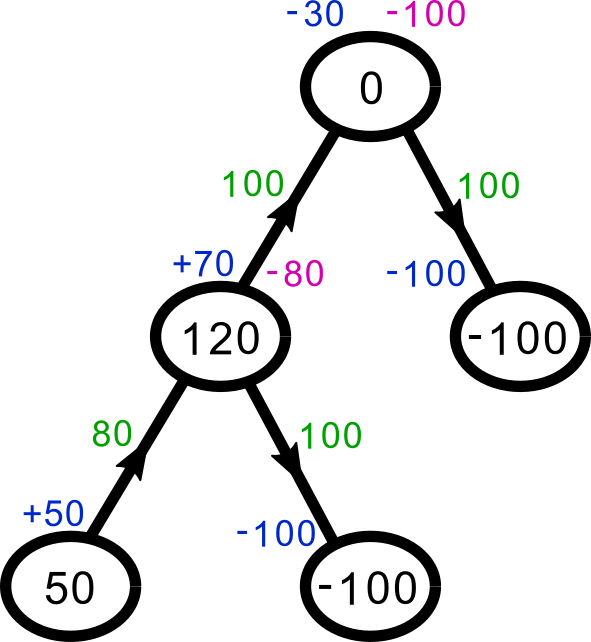
And if it gets so high that it can single handedly satisfy all of the demand, the flow from the bottom-left node stops:
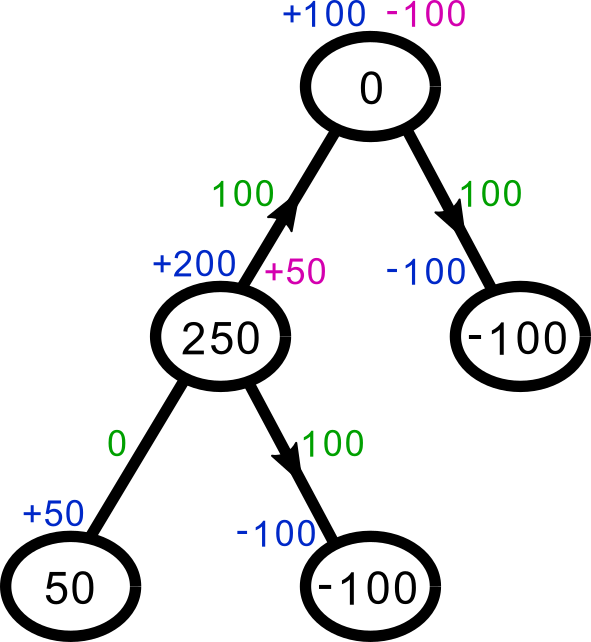
I haven’t proven this solution correct, but I’m pretty sure it is.
Pesky Implementation Details
This section is about how I implemented this algorithm in Factorio. It’s likely not to make much sense if you haven’t played a lot of modded Factorio. In particular, the Space Exploration and AAI Signal Transmission mods. Ok honestly this section might be mostly for my co-players and future self.
Checkpoints
There’s a fundamental difficulty with routing, which is that it’s damn hard to keep track of stuff in an interplanetary factory. If there’s 1743 imersium plates on a spaceship headed to Willownezz, how do you know? If you don’t know, you’re liable to send an additional 1743 plates even if they’re not needed. One way to keep track would be to put a signal transmitter on each spaceship, but those are both large and power hungry. Another option would be to have a counter (SR latch) for each spaceship, but that gets tedious, especially if you have multiple spaceships on the same edge. Oh, and it’s not just spaceships, it’s also trains using your space elevators.
My solution to this is to add checkpoints that separate regions. Every location gets a region, which is the portion of the interplanetary routing system in which items get counted towards its tally. For example, a spaceship en route from Nauvis to Willownezz is in some region: either Nauvis’ region or Willownezz’s region, depending on how you split things up.
Every single item that passes from one region to another must go through a checkpoint, and the checkpoint increments and decrements counters which keep track of the total amount of stuff in each region. The only downside to this is that it means there’s absolutely no stealing or (worse) gifting allowed, as that would invalidate the counts.
There’s a choice of where exactly to draw the lines between regions. I believe a good convention is that the region around a location includes everything being sent to that location. For example, when the factory places an item in a train or spaceship heading to Nauvis Orbit, it increments the item counter for Nauvis Orbit.
To Flow or not To Flow
This checkpoint system means that the destination counter is immediately incremented without long delays for transit time. As a result, we don’t need to know how much to send all at once, just when to turn the tap on or off. Thus when implementing this algorithm in Factorio, it suffices to have filter inserters that filter based on when the computed flow is positive.
Leaf-to-leaf
I only talked about sending resources up and down the tree. But actually this solution allows you to send things directly from one leaf to another. There’s nothing tricky about it: you send iff the destination has a demand, and you need checkpoints as usual. (They do have to both be leaves, though. If you start sending stuff every which way and make the tree problem into a graph problem, things will break.)
Signals
Each location L has three transmitted signals (AAI Signal Transmission signals, not circuit signals):
L Counter: counts items in transit to/thru L. You pulse positive or negative numbers of resource types onto this channel, and it increases/decreases the counts.L Supply-Demand: the total supply of L’s subtree, minus its total demand. (A.k.a. it’s surplus or deficit.)L Satisfaction: the satisfaction of L, as defined above.
Overall Requirements
Putting this all together, a complete routing system looks like this:
- Every location has a counter (SR) circuit that keeps track of its total contents, as well as circuits to compute its Supply-Demand and Satisfaction, as defined above.
- Each location that has supply or demand should add it to its Supply-Demand signal. Positive is supply, negative is demand. If you want to receive items faster, increase your demand. If you want to send items out faster, increase your supply.
- To receive items at a location A: decrement A’s counter, then do what you will with the items.
- To send items from a parent A to its child B: filter on B’s deficit. Decrement A’s counter and increment B’s counter.
- To send items from a child B to its parent A: filter on items for which B has a surplus and A has a dissatisfaction. If B is not a leaf, decrement its counter. Decrement A’s counter.
- To send items from a leaf A to another leaf B: filter on B’s deficit. Increment B’s counter.
- As an annoying detail, filter inserters only have ~4 filter slots. If you want to transfer 27 item types, and 7 of them are out of stock, and the filter inserters’ filter slots get set to some of those 7, they’re not going to transfer anything. Thus you need to filter on item types in the flow that are also available to pick up.
- Absolutely no stealing or gifting!
Here’s a blueprint.
