Pixel to Hex

If you make a game or other application with a hex grid in it, one of the problems you run into is telling what hex your cursor is on. You need to convert from screen coordinates to hex coordinates.

I just found an elegant way to do this, that I haven’t seen elsewhere. It’s the simplest branchless approach I’ve seen.

Integer Hex coordinates

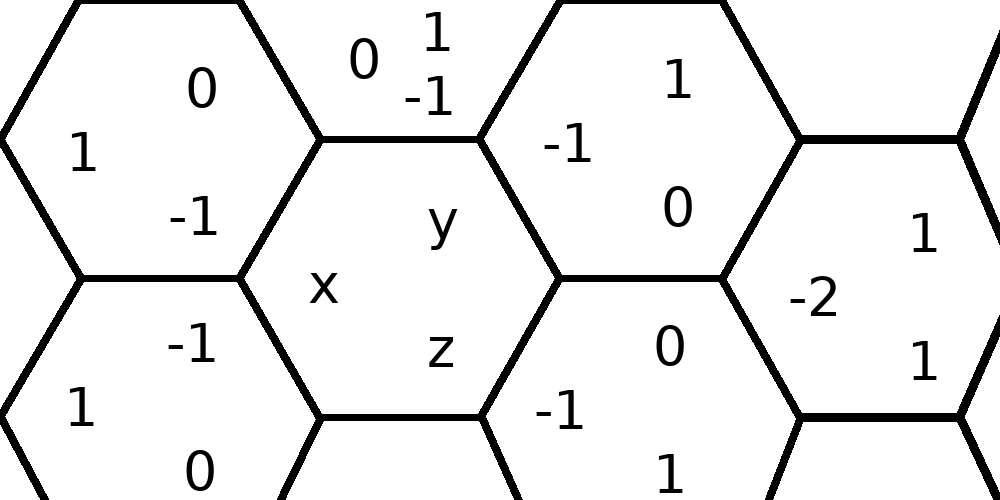
Our end goal is to determine which hexagon the cursor is on, so we need some way to name the hexagons—a coordinate system. There are many coordinate systems for hex tilings. We’ll use the one that Red Blob Games calls cube coordinates. (Everything on that site is golden.)

On a square grid, you can get a coordinate system by labeling each square with its row and column number. On a hex grid, there are three orientations of “rows”. To get a coordinate system, we’ll label each hex (x, y, z) where x is the column, y is the left-slanted-row, and z is the right-slanted row.

Here’s what this coordinate system looks like, where the hex with “x, y, z” in it is the origin hex:

You might notice that we managed to use three numbers to label hexagons arranged on a plane, despite there being only two degrees of freedom. As a result, there’s an invariant: x + y + z = 0.

Fractional Hex coordinates

If instead of using integers (x, y, z) we use floats (fx, fy, fz), then we can extend this coordinate system to be able to name a point on the plane, rather than a hex.

The relationship between fractional hex coordinates and integer hex coordinates is that (for example) the point (fx, fy, fz) = (-1.0, 1.0, 0.0) is the center of the hex (x, y, z) = (-1, 1, 0). Integer coordinates name hexes; fractional coordinates name points.

Satisfyingly, these fractional coordinates also obey the invariant that fx + fy + fz = 0.0.

Step 1: Convert cursor position to fractional hex coordinates

Now let’s say your cursor is at this star, and we want to figure out the (integer!) coordinates of the hex it’s on:

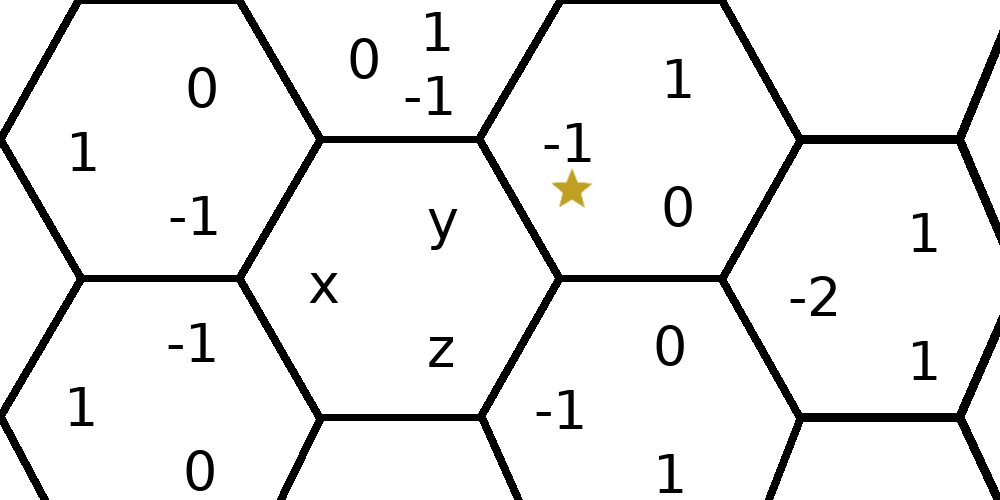
The first step is to convert the cursor position to fractional hex coordinates. This is easy; it’s a linear transformation:

cx = cursor_x / hex_size
cy = cursor_y / hex_size

fx = (-2/3) * cx
fy = (1/3)  * cx  +  (1/sqrt(3)) * cy
fz = (1/3)  * cx  -  (1/sqrt(3)) * cy

(hex_size is the distance from the center of a hex to one of its corners, in screen units.)

This gives the fractional coordinates (-2/3, 2/3, 0) for the star.

Now we just need to convert fractional hex coordinates into integer hex coordinates. You’d think this would be easy, but it’s not. The obvious thing to do is to round x, y, and z to the nearest integer. Rounding like this works for a square coordinate system, but it doesn’t work for hexes.

The trouble is that, even though the fractional hex coordinates obey fx + fy + fz = 0.0, after rounding they might not. And if this invariant is violated, the coordinate isn’t even valid; it isn’t clear which hex it’s supposed to be referencing. (This isn’t merely a floating-point rounding issue. It applies to real numbers too. The rounding simply doesn’t work.)

Red Blob Games gives a nice way to patch up this rounding issue. But it uses a couple of if statements, and that just won’t do. We’re going to do it branchless.

Step 2: Convert from fractional hex coordinates to integer triangle coordinates.

The trick will be to divide the hexes up into triangles, and first determine which of these triangles we’re in. We’ll call our new triangle coordinates a, b, and c, which tell which left-slanted-column, row, and right-slanted-column the triangle is in, respectively. This is similar to the hex coordinates, but rotated.

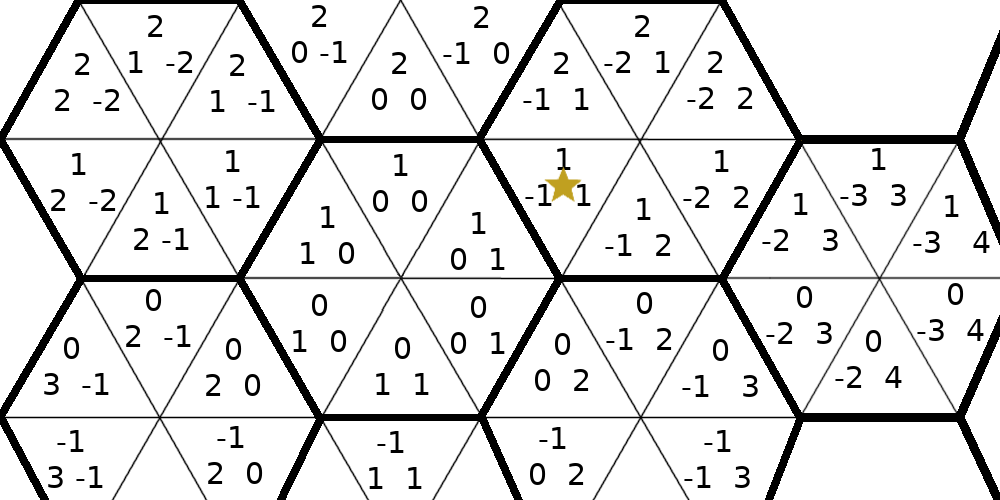
Converting from fractional hex coordinates (fx, fy, fz) to integer triangle coordinates (a, b, c) happens to be very easy:

a = ceil(fx - fy)
b = ceil(fy - fz)
c = ceil(fz - fx)

This gives (a, b, c) = (ceil(-4/3), ceil(2/3), ceil(2/3)) = (-1, 1, 1), which you can see is the correct triangle.

Step 3: Convert back to hex coordinates

Finally, we have to figure out which hex the triangle we’re on is part of. To do this, take the differences of a, b, c and divide by 3:

x = round((a - c) / 3)
y = round((b - a) / 3)
z = round((c - b) / 3)

We get (x, y, z) = (round(-2/3), round(2/3), round(0)) = (-1, 1, 0).

And that’s it! We have integer hex coordinates that obey the invariant x + y + z = 0, and tell us exactly which hex we’re on.

Questions

Why ceil?

Actually floor works too. You just have to go one way or the other because the center of the origin hex [fx, fy, fz] = [0.0, 0.0, 0.0] is at the boundary of six triangles.

Why divide by 3?

Look at what happens to the center of a hex where [fx, fy, fz] are all integers:

a = ceil(fx - fy) = fx - fy
b = ceil(fy - fz) = fy - fz
c = ceil(fz - fx) = fz - fx

a - c = (fx - fy) - (fz - fx)
      = 2fx - fy - fz
      = 3fx   // adding fx + fy + fz = 0

x = round((a - c) / 3) = round(3fx / 3) = fx

---

Thanks to Evan, for reading a draft of this post.